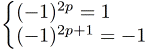Page personnelle de Pierre Chatelier

Méta-programmation Ou comment faire calculer factorielle, puissance, sinus, cosinus, π, arctangente hyperbolique... à un pré-processeur C++. Sommaire - Explications - Implémentations Puissance Factorielle Exponentielle Sinus Arcsinus Cosinus Arccosinus Tangente Arctangente Sinus hyperbolique Cosinus hyperbolique Tangente hyperbolique Arctangente hyperbolique π - Opimisations - Tests (attention : page à part, lourde à charger) π Exponentielle Sinus Arcsinus Cosinus Arccosinus Tangente Arctangente Sinus hyperbolique Cosinus hyperbolique Tangente hyperbolique Arctangente hyperbolique Téléchargement

Explications

Définition

D'abord, que signifie le préfixe "meta" ? Pour simplifier, je vais juste donner la définition suivante :

Un méta-truc, c'est un machin qui est une description du truc.

Application à l'informatique

Loin de moi l'idée d'appliquer cette définition à des termes tels que "métaphysique", mais elle est parfaite pour le domaine informatique.
Dans un langage object, une classe est un méta-objet : elle le décrit. Dans certains langages objets, on peut même voir apparaître la notion de méta-classe. (Notion effleurée en C++ grâce aux attributs static qui sont en fait des attributs de classe, ce qui laisse entrevoir qu'une classe peut elle aussi être vue comme un objet.)
Un code source, c'est un méta-exécutable. Il est censé décrire le comportement de la machine. L'étape de compilation instancie ce code source. La méta-programmation, quant à elle, est une étape encore en amont. Elle instancie du code source pendant une phase de pré-processing, (lequel code s'instancie ensuite en binaire exécutable...).
Typiquement, une macro en C permet de faire de la méta-programmation, puisqu'elle est est remplacée par du code source pendant le pré-processing.

#define MAX(A,B) ((A>B)?A:B)
int main(int, char**)
{
  int x=0;
  int y=1;
  printf("%d\n",MAX(x,y));
  return 0;
}

Pré-compilation

int main(int, char**)
{
  int x=0;
  int y=1;
  printf("%d\n",((x>y)?x:y));
  return 0;
}

Fig. 1 : La macro est transformée en code

En étant un peu malin, il est parfois possible d'éviter de taper du code, en le faisant se générer par une technique de métaprogrammation. Reprenons la macro MAX(A,B). Elle donnera des résultats incorrects si on l'utilise via MAX(x++,y). C'est le problème des effets de bord. A la place d'une macro, il faudrait une fonction. Cependant, en C, la surcharge n'existe pas, il faudrait donc écrire le code de différentes fonctions

int max_int(int,int),
long max_long(long,long),
double max_double(double,double)
...

Cela est long, cela génère de la redondance de code : bref, beaucoup d'inconvénients... sauf si on fait appel à la métaprogrammation!
Considérez le code suivant; on ne tape le code de MAX qu'une seule fois, mais il est utilisé pour int et double:

/* (Rappel : '##' est un opérateur de concaténation au pré-processing) */
#define DEFINE_MAX(TYPE) TYPE Max_##TYPE##(TYPE x, TYPE y) { return (x>y) ? x : y;}

DEFINE_MAX(int)
DEFINE_MAX(double)

int main(int, char* [])
{
  int n=1;
  int m=2;
  double x=0.123;
  double y=0.456;

  printf("max(n,m)=%d\n",Max_int(n,m));
  printf("max(x,y)=%f\n",Max_double(x,y));

  return 0;
}

Pré-compilation

int Max_int(int x, int y) { return (x>y) ? x : y;}
double Max_double(double x, double y) { return (x>y) ? x : y;}

int main(int, char* [])
{
  int n=1;
  int m=2;
  double x=0.123;
  double y=0.456;

  printf("max(n,m)=%d\n",Max_int(n,m));
  printf("max(x,y)=%f\n",Max_double(x,y));

  return 0;
}

Fig. 2 : Multiples instanciations d'une fonction.

C'est bien là l'idée de la métaprogrammation : écrire du code à notre place, avec tous les avantages que cela comporte.

C++, inlining et templates

Le petit problème de MAX(int,int) et MAX(double,double) résolu ci-dessus est valable pour du C, pas pour du C++ où les templates sont un bien meilleur moyen d'arriver à ses fins. Et justement : l'utilisation conjointe de templates et d'inlining est extrêmement puissante, et permet de se passer des macros, pour réaliser des choses assez exceptionnelles. Par exemple, comme vous le verrez plus bas, on peut faire calculer π, ou 10!, ou encore arctanh(0.123), et beaucoup d'autres choses... au préprocesseur!

Le pré-calcul de valeurs

A quoi cela sert-il de faire calculer sin(30) au préprocesseur? Pour la lisibilité et la rapidité d'exécution.

Supposons un code dans lequel vous ayez besoin de sin(30). Vous pouvez écrire

x = sin(30); //prends du temps à l'exécution

ou bien

x = -0.9880316240928618; //pas très pratique

D'habitude, on utilise des tables de valeurs précalculées. On pourrait ainsi écrire

x = sinus[30]; //sinus est un tableau précalculé

L'inconvénient est qu'il faut justement initialiser la table, faire attention aux débordements d'indice... Si cette table est nécessaire pour plusieurs fichiers sources, il faut la déclarer plusieurs fois et la définir dans un fichier qui devra être compilé et inclus lors de l'édition des liens... Bref, cela demande du travail préliminaire, qui est parfois un peu pénible. Cela reste malgré tout une excellente solution dès que l'on a besoin d'un jeu important de constantes pré-calculées.

Une autre solution serait de bénéficier d'une sorte de "macro" SINUS, qui serait evaluée à la compilation, et serait donc aussi efficace que d'avoir écrit directement la valeur dans le code. Il serait sympathique de pouvoir écrire:

x = SINUS(30); //Non, ce n'est pas de la science-fiction! Vous le verrez plus loin.

Instanciation récursive de templates

Pour comprendre comment nous allons nous y prendre, l'exemple le plus simple est encore la fonction factorielle. (n! = n*(n-1)*(n-2)*...*1)

Un paramètre template n'est pas forcément un type, ce peut être un entier. De ce fait on peut écrire:

      template<unsigned int N> inline Fact() {return N*Fact<N-1>();}

Cela pourrait marcher mais il faut prévoir de terminer la récursion en faisant une spécialisation du template pour N=0.

      template<unsigned int N> inline Fact() {return N*Fact<N-1>();}
      template<> inline Fact<0>() {return 1;}

A la compilation, Fact<5>() devient 5*Fact<4>(), à nouveau déroulé en 5*4*Fact<3>(), etc., jusqu'à obtenir 5*4*3*2*1, que le compilateur sait alors évaluer en 120. Le fait de demander l'inlining n'est pas anodin, car ce code serait sinon terriblement inefficace: il ne serait pas inliné, et se transformerait en une succession d'appels de fonctions, bien moins rapides qu'une simple boucle:

unsigned int result = 1;
while(n)
{
  result *= n;
  --n;
}

Terminaison de la récursion

La terminaison de la récursion est très particulière. Nous avons préféré écrire

template<int N> inline Fact() {return N*Fact<N-1>();}
template<> inline int Fact<0>() {return 1;}

au lieu d'un simple

      template<int N> inline Fact() {if (N==0) return 1; else return N*Fact<N-1>();}

En effet, dans ce dernier cas, le mécanisme d'inlining ne serait pas stoppé, car Fact<0>() est déroulé en

      if (0==0) return 1; else return 0*Fact<-1>();

Et le compilateur doit alors résoudre Fact<-1>(), qui va nécessiter Fact<-2>(),... jusqu'à l'infini. Le compilateur va alors s'arrêter avec un message du genre "too many levels of recursion" (trop grande profondeur de récursion).

Pour les mêmes raisons, on ne s'en sort pas avec l'opérateur "?:", car les deux arguments seront bien évalués.

      template<unsigned int N> inline Fact()
      {
        return (N ? 1 : N*Fact<N-1>()); //ne fonctionne pas non plus
      }

La solution qui semble s'imposer serait donc :

template<int N> inline Fact() {return N*Fact<N-1>();}
template<> inline int Fact<0>() {return 1;}

Et pourtant, nous allons voir que ce n'est pas satisfaisant.

Cela pose en effet un grave problème. Imaginons que l'on veuille également rendre la factorielle template par rapport au type de retour. Ce serait une bonne chose, car pour les petits nombres, on aurait un résultat exact via Fact<N,unsigned long>, et pour les grands nombres, il faudrait passer par Fact<N,double>. (Sinon, les unsigned long subissent le débordement (overflow) et donnent un résultat incorrect).

Il n'est pas possible en C++ de faire de la semi-spécialisation de template. On ne pourrait donc PAS écrire

      template<unsigned int N,typename T> inline Fact() {return N*Fact<N-1>();}
      template<0,typename T> inline Fact<0,T>() {return 1;} //syntaxe impossible

Il nous faut pourtant stopper la récursion hors du code de calcul !

L'astuce consiste à se passer de la spécialisation en 0 grâce à une acrobatie peu lisible mais efficace. Il suffit de mettre des conditions à l'intérieur même du paramètre template.

template<int N> inline Fact()
{
  return (N==0) ? 1 : N*Fact<(N==0)?1:N-1>();
}

Grâce à cette astuce, Fact<0> est déroulé en:

     return (0==0) ? 1 : 0*Fact<0>(); //Fact<0> peut alors être résolu,
                                      //et est évalué à la valeur "1"

Notre fonction factorielle définitive sera donc:

template<unsigned long N,typename T> inline Fact()
{
  return (N==0) ? 1 : N*Fact<((N==0)?1:N-1),T>();
}

Pour l'utiliser, on fera des appels de ce genre:

  unsigned int x = Fact<5,unsigned int>(); //5!
  unsigned int y = Fact<50,unsigned int>(); //50! le résultat sera sans doute incorrect
                                            //à cause du débordement en calcul entier
  double z = Fact<50,double>(); //50! le résultat sera une valeur approché

Sinus, cosinus, arctan... comment faire?

J'annonçais au début que le préprocesseur pouvait calculer un sinus. Nous venons de voir que si le sinus avait une formule "récursive", ce serait sans doute possible. Et en effet, pour cela j'ai utilisé le développement en série entière (DSE). Ainsi, le sinus s'exprime de façon itérative, ce qui se transforme aisément en un calcul récursif.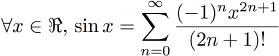

Fig. 3 : développement en série entière du sinus

J'ai donc implémenté en template-inline plusieurs fonctions dont je connais le développement en série entière (DSE): sinus, cosinus, tangente, arcsinus, arccosinus, arctangente, sinus hyperbolique, cosinus hyperbolique, tangente hyperbolique, arctangente hyperbolique, exponentielle.

Les DSE nécessitent les fonctions puissance et factorielle que je fournis également. Les fonctions trigonométriques nécessitent aussi parfois π. J'ai également trouvé une formule itérative de π, qui converge assez vite pour justifier sa présence parmi les autres fonctions.

À chaque fois, le paramètre template est l'ordre jusqu'auquel il faut développer la série. (Plus il est important, plus le calcul est précis). Il faut cependant faire attention au rayon de convergence des séries. Par exemple, la formule utilisée pour arctangente a un rayon de convergence de 1. Ce qui signifie qu'elle est valable pour |x|<1. Avec une astuce, on peut l'adapter pour |x|≠1, mais elle sera inefficace pour 1 et -1.

Les DSE que j'utilise correspondent généralement au développement limité en 0, ce qui signifie en pratique que plus x est proche de 0, plus rapide sera la convergence. En d'autres termes, il faudra souvent augmenter l'ordre avec la valeur absolue de x. La partie Tests sert de référence pour la relation entre l'ordre, l'abcisse et la précision désirée.

Implémentations

[Puissance][Factorielle] [Exponentielle] [Sinus][Arcsinus] [Cosinus][Arccosinus] [Tangente][Arctangente] [Sinus hyperbolique] [Cosinus hyperbolique] [Tangente hyperbolique] [Arctangente hyperbolique] [π]

Puissance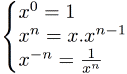

Cette formule est correcte, mais il faut l'optimiser. Voyez la partie optimisations pour vous en convaincre. Pour optimiser, on remarque que

Ceci permet de faire tomber la profondeur de récursivité de manière non négligeable. Le code correspondant est:

//Metaprog_sqr
//Utilitaire, calcule x*x / utility, computes x*x
template<typename T> static inline T Metaprog_sqr(T x) {return x*x;}

//Pow<P,T>(T x) = x^P.
//Pas de restriction particulière/There are no special restrictions
template <int P,typename T>
inline T Pow(T x)
{
  return (P == 0) ? 1
                  : (
                     (P<0) ? 1/Pow<(P<0)?(-P):0,T>(x)
                           : ((P%2) ? x*Metaprog_sqr(Pow<(P%2)?((P-1)/2):0,T>(x))
                                    : Metaprog_sqr(Pow<(P%2)?0: P/2,T>(x))
                             )
                    );
}
//end Pow<>()

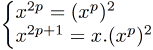
Notez bien les passages

(P<0) ? 1/Pow<(P<0)?(-P):0,T>(x)"
Pow<(P%2)?((P-1)/2):0,T>(x)
Pow<(P%2)?0: P/2,T>(x)

Nous avons vu que les tests à l'intérieur des paramètres template n'étaient pas équivalents à des tests dans le code. Ici, une optimisation non négligeable (voire fondamentale) est faite : les tests des paramètres template court-circuitent ou élaguent au maximum les branches d'instanciation, en profitant de la relation sur les puissances paires et les puissances impaires. Le jeu en vaut réellement la chandelle.

Utilisation

int x = Pow<10>(2); //2^10
double y = Pow<-10>(1.); //1^(-10)

Factorielle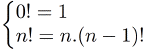

Le code correspondant est:

//Fact<N,T>() = N*(N-1)*(N-2)*(N-3)*...*1 (result of type T)
//Attention : Si N est grand, un type integral pour T peut subir le debordement
//Caution : for a great N, an integral type for T may overflow 
template<unsigned long N,typename T>
inline T Fact()
{
  return (N==0) ? 1 : N*Fact<(N > 0 ? N-1 : 0),T>();
}
//end Fact<>()

Utilisation:

int x = Fact<10,int>(); //10!
double y = Fact<50,double>(); //50!

Exponentielle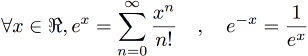

exp(x)=1+x/1+x^2/2!+x^3/3!..., exp(-x)=1/exp(x)

Le code correspondant est:

//Exp_ est juste un intermediaire de calcul/
//Exp_ is just an intermediary of calculation
template<unsigned int N>
inline double Exp_(double x)
{
  return (N==0) ? 1 : Exp_<(N>0)?(N-1):0>(x)+Pow<N,double>(x)/Fact<N,double>();
}
template<unsigned int N>
//Exp
//Pas de restriction particulière/No special restrictions
inline double Exp(double x) {return (x>=0) ? Exp_<N>(x) : (1/Exp_<N>(-x));}

J'ai constaté que le DSE utilisé converge vite vers la bonne valeur pour les x positifs, mais pas pour les x négatifs. C'est pour cela que je passe par l'astuce e^-x = 1/e^x, car elle est très efficace, voire indispensable au vu des résultats obtenus. Ne pas l'utiliser implique de mettre un TRÈS grand ordre de récursion, ce qui est une mauvaise solution. Cependant, elle nécessite de séparer les deux cas x≤0 et x≥0, et du coup, la fonction Exp<> génère systématiquement deux branches d'instanciation avec Exp_<N>(x) et 1/Exp_<N>(-x).

Cela est malheureusement assez inévitable. J'avais pensé à deux méthodes pour y couper, mais elles sont en fait impossibles:

template<unsigned int N> inline double Exp(double x)
{
  return (x>=0) ? Exp_<(x>=0)?N:0>(x) :
       (1/Exp_<(x<0)?N:0>;
}//ne compile pas

template<unsigned int N> inline double Exp(double x)
{
  return Pow<(x>=0)?1:-1>(Exp_<N>((x>=0)?x:-x));
}//ne compile pas

En effet, étrangement, on ne peut effectuer que des tests "intégraux" (i.e. avec des type dits "exacts", comme int, bool...) dans le paramètre template. Le compilateur refuse d'évaluer "x>=0" entre les chevrons du template, car x n'a pas une représentation binaire exacte comme en ont les entiers ou les booléens.

Utilisation

double x = Exp<10>(3); //exp(3), pas très précis (ordre 10)
double x = Exp<30>(3); //exp(3), assez précis (ordre 30)

La question de la précision est intéressante. J'ai effectué toutes sortes de tests pour connaître l'ordre de développement nécessaire à une précision donnée. On les trouve dans la partie Tests.

Sinus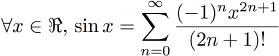

Le code correspondant est:

//Sin
//Pas de restriction particulière/No special restrictions
//Pour une bonne precision, garder x dans [-2*pi,2*pi]/
//For a good precision, keep x in [-2*pi,2*pi]
template<unsigned int N>
inline double Sin(double x)
{
  return (!(N%2)) ? Sin<(!(N%2))?N-1:0>(x)
                  : Sin<(N%2)?N-2:0>(x) +
                    ((((N-1)/2)%2)?-1:1)*Pow<(N%2)?N:0,double>(x)
                                        /Fact<(N%2)?N:0,double>();
}
template<> inline double Sin<1>(double x) {return x;}
template<> inline double Sin<0>(double x) {return 0;}
//end Sin

Il y a trois choses à remarquer:

D'abord, il a fallu faire un changement de variable N=2n+1 pour écrire la récurrence et jouer sur les indices pairs et les indices impairs.
Ensuite, il y a l'astuce de

qui permet de considérablement réduire le calcul.
Enfin, (et surtout), il faut répéter les tests de parité de N dans tous les paramètres templates, pour élaguer les branches d'instanciation inutiles. Cette optimisation est loin d'être négligeable, et fait gagner énormément de mémoire, donc de temps de compilation.

Le rayon de convergence de ce DSE est infini, ce qui signifie qu'il est correct pour tout x. Cependant, plus x est éloigné de 0, plus la convergence est lente. Je conseille donc de garder x dans [-2π ; 2π], pour que cela reste pratique tout en étant efficace. Voyez les tests pour vous faire une idée plus précise.

Utilisation:

double x = Sin<5>(0.123); //sin(0.123) pas très précis (ordre 5)
double x = Sin<15>(0.123); //sin(0.123) assez précis (ordre 15)

Arcsinus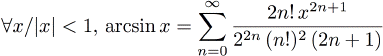

Le code correspondant est:

//asin
//Requis : |x|<1 / Requires : |x|<1
//INCORRECT avec |x|=1 / INCORRECT for |x|=1
template<unsigned int N>
inline double asin(double x)
{
  return (!(N%2))?asin<(!(N%2))?N-1:0>(x)
                 :asin<(N%2)?N-2:0>(x)+(Fact<(N%2)?N-1:0,double>()*
                                        Pow<(N%2)?N:0,double>(x))/
                                       (Pow<(N%2)?N-1:0,double>(2)*
                                        Metaprog_sqr(
                                          Fact<(N%2)?(N-1)/2:0,double>())*N);
}
template<> inline double asin<1>(double x) {return x;}
template<> inline double asin<0>(double x) {return 0;}
//end asin

Notez que le rayon de convergence est strictement inférieur à 1. Cela signifie que la formule est incorrecte pour |x|=1. Cependant, on sait que arcsin(1)=π/2 et arcsin(-1)=-π/2. L'arcsinus n'est pas défini pour |x|>1

Utilisation:

double x = asin<30>(0.56789); //arcsin(0.56789)

Cosinus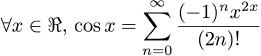

Le code correspondant est:

//Cos
//Pas de restriction particulière/No special restrictions
//Pour une bonne precision, garder x dans [-2*pi,2*pi]/
//For a good precision, keep x in [-2*pi,2*pi]
template<unsigned int N>
inline double Cos(double x)
{
  return (N%2) ? Cos<(N%2)?N-1:0>(x)
               : Cos<(N%2)?0:N-2>(x) + 
                 (((N/2)%2)?-1:1)*Pow<(N%2)?0:N,double>(x)/Fact<(N%2)?0:N,double>();
}
template<> inline double Cos<1>(double x) {return x;}
template<> inline double Cos<0>(double x) {return 1;}
//end Cos

Tout comme pour le sinus, la convergence est rapide avec un x petit.

Utilisation:

double x = Cos<15>(0.31415927); //cos(0.31415927)

Arccosinus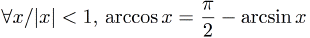

Le code correspondant est:

//acos
//Requis : |x|<1 / Requires : |x|<1
//INCORRECT avec |x|=1 / INCORRECT for |x|=1
template<unsigned int N>
inline double acos(double x)
{
  return (pi/2)-asin<N>(x);
}
//end acos

Notez que le lien avec l'arcsinus implique que là encore, le rayon de convergence étant strictement inférieur à 1, la formule est incorrecte pour |x|=1. Cependant, on sait que arccos(1)=0 et arccos(-1)=π. L'arccosinus n'est pas défini pour |x|>1

Utilisation:

double x = acos<30>(0.56789); //arccos(0.56789)

Tangente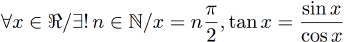

Le code correspondant est:

//Tan
//Pas de restriction particulière (a part x != n*Pi/2) /
//No special restrictions (but x != n*Pi/2)
//Pour une bonne precision, garder x dans [-2*pi,2*pi]/
//For a good precision, keep x in [-2*pi,2*pi]
template<unsigned int N> inline double Tan(double x)
{
  return Sin<N>(x)/Cos<N>(x);
}
//end Tan

Utilisation:

double x = Tan<30>(3.1415927); //tan(3.1415927)

Arctangente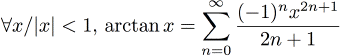

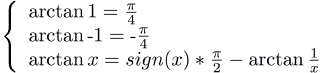
arctan(+-1)=+-π/4,arctan(x)=+-π/2-arctan(1/x)

Le code correspondant est:

//atan
//Eviter les valeurs poches de +-Pi/4 / Avoid values close to +-Pi/4
template<unsigned int N> inline double atan(double x)
{
  return ((x >= -1-(1e-10)) && (x<=-1+(1e-10))) ? -pi/4
                        : ((x >= 1-(1e-10)) && (x<=1+(1e-10))) ? pi/4
                             : ((x<-1) || (x>1)) ? ((x<=-1)?-1:1)*pi/2-atan<N>(1/x)
                                        : (!(N%2)) ? atan<(!(N%2))?N-1:0>(x)
                                              : atan<(!(N%2))?0:N-2>(x)+
                                                ((((N-1)/2)%2)?-1:1)*
                                                  Pow<(!(N%2))?0:N>(x)/N;
}
template<> inline double atan<1>(double x) {return x;}
template<> inline double atan<0>(double x) {return 0;}
//end atan

Le fait de donner des valeurs proches de π/4 fait dramatiquement baisser la précision à un ordre donné. Cette formule est assez problématique, comme vous pouvez le constater dans les tests. De plus, la séparation de cas nécessaire sur la valeur de x implique la création de plusieurs branches d'instanciations, ce qui fait perdre du temps et de la mémoire.

Utilisation:

double x = atan<30>(0.1); //atan(0.1)

Sinus hyperbolique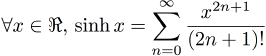

Le code correspondant est:

//Sinh
//Pas de restriction particulière/No special restrictions
template<unsigned int N>
inline double Sinh(double x)
{
  return (!(N%2)) ? Sinh<(!(N%2))?N-1:0>(x)
                  : Sinh<(!(N%2))?0:N-2>(x) +
                    Pow<(!(N%2))?0:N,double>(x)/Fact<(!(N%2))?0:N,double>();

}
template<> inline double Sinh<1>(double x) {return x;}
template<> inline double Sinh<0>(double x) {return 0;}
//end Sinh

Utilisation:

double x = Sinh<15>(0.31415927); //sinh(0.31415927)

Cosinus hyperbolique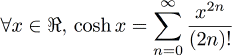

Le code correspondant est:

//Cosh
//Pas de restriction particulière/No special restrictions
template<unsigned int N>
inline double Cosh(double x)
{
  return (N%2) ? Cosh<(N%2)?N-1:0>(x)
               : Cosh<(N%2)?0:N-2>(x) +
                 Pow<(N%2)?0:N,double>(x)/Fact<(N%2)?0:N,double>();
}
template<> inline double Cosh<1>(double x) {return 0;}
template<> inline double Cosh<0>(double x) {return 1;}
//end Cosh

Utilisation:

double x = Cosh<15>(0.31415927); //cosh(0.31415927)

Tangente hyperbolique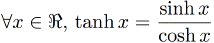

Le code correspondant est:

//Tanh
template<unsigned int N> inline double Tanh(double x)
{
  return Sinh<N>(x)/Cosh<N>(x);
}
//end Tanh

Utilisation:

double x = Tanh<15>(0.31415927); //tanh(0.31415927)

Arctangente hyperbolique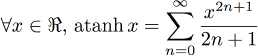

Le code correspondant est:

//atanh
//Pas de restriction particulière/No special restrictions
template<unsigned int N> inline double Atanh(double x)
{
  return (!(N%2)) ? Atanh<(!(N%2))?N-1:0>(x)
                  : Atanh<(!(N%2))?0:N-2>(x)+Pow<(!(N%2))?0:N>(x)/N;
}
template<> inline double Atanh<1>(double x) {return x;}
template<> inline double Atanh<0>(double x) {return 0;}
//end Atanh

Utilisation:

double x = Atanh<15>(0.31415927); //atanh(0.31415927)

π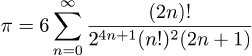

Parmi plusieurs formules de calculs de π, celle-ci (une méthode dite "de Newton") a une convergence très rapide et est très statisfaisante. J'en ai essayé d'autres qui se comportaient moins bien.

Le code correspondant est:

//Pi_ est juste un intermediaire de calcul/
//Pi_ is just an intermediary of calculation
template<unsigned int N>
inline double Pi_(void)
{
  return Pi_<N-1>()+Fact<2*N,double>()/
                          (Pow<4*N+1,double>(2)*
                           Metaprog_sqr(Fact<N,double>())*(2*N+1));
}
template<> inline double Pi_<0>(void) {return 1/double(2);}

//Pi
//Pas de restriction particulière/There is no special restriction
template<unsigned int N> inline double Pi(void) {return 6*Pi_<N>();}

Utilisation:

double pi = Pi<15>(); //bonne approximation

Optimisations Vous avez pu le constater, j'ai essayé au maximum d'optimiser le développement inline, au détriment de la lisibilité. Mais ces optimisations sont réellement nécessaires, sinon les temps de compilation peuvent extrêmement longs. Par exemple pour réaliser des tests, j'avais créé un fichier .cpp instanciant une centaine de tangentes (Tan<N>()), à l'ordre 50. Les templates Pow<>() Sin<>(), Cos<>() étaient écrits de façon "naïve". La compilation durait, durait... Le processus cc1plus (compilateur de gcc) prenait 835Mo de mémoire* et a compilé pendant 775 minutes, soit 13h, sur un Macintosh G4 800Mhz avec 512Mo de RAM. Sur une machine Linux P-IV 2.4Ghz, 512Mo de RAM, le système a rebooté et n'a jamais pu en venir à bout. C'est assez logique, les instanciations en cascades ont généré un fichier source intermédiaire gigantesque, plus gros que la taille de la RAM, et le système passait son temps à swapper. (D'ailleurs, un <top> indiquait que seul 20% du processeur était consacré à au processus cc1plus.) Avec les optimisations élémentaires sur Pow<>(), je suis descendu à 7 minutes de compilation... Avec toutes les optimisations par élagage de branches d'instanciations, on passe à quelques secondes: le jeu en vaut clairement la chandelle.

Tests Les tests sont sur une page à part, car les nombreuses images qui s'y trouvent sont assez longues à charger

Téléchargement

Voir le fichier d'en-tête	: Metaprog.h (8Ko)
Télécharger l'ensemble code+tests	: Metaprog.zip (4Ko)

Sommaire

Définition

Application à l'informatique

Fig. 1 : La macro est transformée en code

Fig. 2 : Multiples instanciations d'une fonction.

C++, inlining et templates

Le pré-calcul de valeurs

Instanciation récursive de templates

Terminaison de la récursion

Sinus, cosinus, arctan... comment faire?

Utilisation

Utilisation:

Utilisation

Utilisation:

Utilisation:

Utilisation:

Utilisation:

Utilisation:

Utilisation:

Utilisation:

Utilisation:

Utilisation:

Utilisation:

Utilisation: